Python判断一个数是否为质数的3种方法(超详细)

(发现好多博客对第三种进阶方法说的不明白，至少我是没完全看明白。后面结合自己的理解应该算是弄懂了，供大家参考，欢迎纠正。)

方法一：最暴力，最简单，也最耗时O(n)

思想：由素数的定义：一个数t，除了1和它本身，若没有其他因数，那么就称其为素数。因此循环i从2开始到t-1，依次判断t是否将i整除，若是则不为素数。

代码：

# 判断是否为质数
def is_zhishu(t):
    if t <= 1:
        # 1和0都不是质数
        return False
    for i in range(null, t):
        if t % i == 0:
            # 整除就是余数为0 只要有一个被整除 就找到因数 就不是质数
            return False
    return True

t = int(input())
print(is_zhishu(t))

方法二：

一个数t，其必然可以拆解为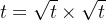,则其整数因数必然一个不大于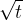,一个不小于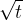.因此可以只搜索小于等于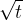的因数即可，将上述代码小改一下即可。此时时间复杂度就只需要O().

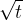代码：

# 判断是否为质数
import math
def is_zhishu(t):
    if t <= 1:
        # 1和0都不是质数
        return False
    sqrt_t = math.ceil(t**0.5)  # 这里用ceil的原因是要取整数才能输入range
    for i in range(null, sqrt_t):
        if t % i == 0:
            # 整除就是余数为0 只要有一个被整除 就找到因数 就不是质数
            return False
    return True

t = int(input())
print(is_zhishu(t))

方法三：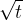

时复<=O().

方法三基于如下一个规律：

首先。对于任一个自然数t，只要t>=5, 则可以写成6x-1,6x,6x+1,6x+2,6x+3,6x+4,...(x>=1)中的任一个。其次，针对上面的这种表达，依次看其是否是质数。

• 6x-1: 不能确定(因为像35=6*6-1不是质数，但41=6*7-1是质数，因此暂时不能确定)
• 6x: 因数可以是2,3,6，必定不是质数
• 6x+1: 不能确定(因为像25=4*6+1不是质数，但37=6*6+1是质数，因此暂时不能确定)
• 6x+2: =2(3x+1)因数可以是2，必定不是质数
• 6x+3: =3(2x+1)因数可以是3，必定不是质数
• 6x+4: =2(3x+2)因数可以是2，必定不是质数

因此，对于t>=5，只有t可以写成t=6x-1或者t=6x+1(x>=1)时才有可能是质数。那么判断t是否可以写成这两种形式该如何体现在代码上呢？

• 首先我们知道代码中t%6 == 1,表示t = 6x+1(x>=0)的t都能识别出来，因此判断t>=5时可以被写成这种形成t=6x+1(x>=1)的就直接用t%6 == 1来判断即可，因为可以被识别出来即可。
• 而t=6x-1(x>=1)，这个-1的要如何识别出来呢？这个直接体现是体现不了在余数上的，因此需要转换一下，t=6x-1(x>=1)等价于t=6(x+1)-1(x>=0)=6x+5(x>=0). 类似上一个所说，t%6 == 5,表示t = 6x+5(x>=0)的t都能识别出来.因此这时只需要用t%6 == 5来识别t=6x-1(x>=1)这种情况即可。

所以代码中将可能是质数的先提取出来。即当t>=5时将不是质数的先判断为False。

前半部分：

if t <= 1 or t == 4:
    return False
elif t == 2 or t == 3:
    return True
    # 至此 先把t<5的情况全部讨论完，再看t>=5有规律的情况
elif t%6 != 1 and t%6 != 5:
    # 这里采用！= 就是将可能为质数的提取出来，！= 的就一定不是质数
    return False

那么接下来就是如何判断t=6x-1或者t=6x+1(x>=1)这两种形式到底是不是质数的问题了。首先我们采用方法二的大方向，这两种数如果不是质数，那么其必定会有一个因数不大于根号t，这样就找到了遍历时的右边界i = 根号t向上取整。那么i是从几开始，间隔又是几递增呢？直接搜会告诉你i从5开始，间隔是6，这是为什么？很多博客中说因为t=6x-1或者t=6x+1(x>=1)，可是这个是t，又不是t的因数。那么为什么t的因数又只有6x-1或6x+1这两种形式呢？请看我细细道来。

• 首先，t=6x-1或者t=6x+1(x>=1)这两种形式的数的因数也只可能为6x-1或者6x+1(x>=1),因为其他数的形式6x,6x+2,6x+3,6x+4(x>=0)(这里如果取6x则x>=1)要么一定有最小因数2要么一定有最小因数3，因此都不可能是t=6x-1或者t=6x+1(x>=1)的因数(这个前面分析过了，因为其不管怎么拆都拆不出2和3).因此对于t=6x-1或者t=6x+1(x>=1)这两种形式的数的因数也只可能为6x-1或者6x+1(x>=1)的形式[这里相当于从5开始了，是因为1不算因数，2和3刚已经说了不可能为t的因数了，4(因为可以拆成2)因此不可能是t的因数了]。所以现在就知道i从5开始！且因为6x-1或者6x+1(x>=1)都有可能成为t的因数，因此每遍历一次i就要有两次判断！(分别针对6x-1和6x+1的，i从5开始即每次取i时就是在判断6x-1(x>=1)，取i+2时就是在判断6x+1(x>=1))，即t%i ==0 or t%(i+2) ==0,一旦有能被整除的就是False。现在i递增是6就很容易理解了，第一轮x=1时6x-1=5;判断完后第二轮x=2时6x-1 = 6(x-1)-1+6,因此每次递增6就可以将6x-1(x>=1)刚好全部判断完。
• 没有然后了，已经结束，看不懂慢慢读多读几遍首先那一段就OK，不要着急。

方法三的完整代码：

import math
def is_zhishu(t):
    # 先把小于5的所有情况讨论完
    if t <= 1 or t == 4:
        return False
    elif t in (null,3):
        return True
    # 至此 t都是>=5的情况，这时就可以把t不是=6x-1,6x+1(x>=1)这两种情况过滤掉
    elif t%6 != 1 and t%6 != 5:
        return False
    # 此时基于t>=5基础上把有可能是质数的t=6x-1or6x+1(x>=1)的两种情况提取出来
    # 按照前面所说遍历i从5开始，递增6，至sqrt_t去寻找其因数,每轮要识别i(对应6x-1这种因数)和(i+2)(对应6x+1这种因数)
    sqrt_t = math.ceil(t**0.5)
    for i in range(null, sqrt_t, 6):
        if t % i == 0 or t %(i+2) == 0:
            return False
    return True

t = int(input())
print(is_zhishu(t))

总结 

到此这篇关于Python判断一个数是否为质数的3种方法的文章就介绍到这了,更多相关Python判断一个数为质数内容请搜索插件窝以前的文章或继续浏览下面的相关文章希望大家以后多多支持插件窝！